Exact Adaptable Radial Axes (ARA) mappings using the L2 norm

ara_exact_l2() computes exact Adaptable Radial Axes (ARA) mappings for the L2 norm

Usage

ara_exact_l2(X, V, variable = 1, solver = "formula")

Arguments

X: Numeric data matrix of dimensions N x n, where N is the number of observations, and n is the number of variables.
V: Numeric matrix defining the axes or "axis vectors". Its dimensions are n x m, where 1<=m<=3 is the dimension of the visualization space. Each row of V defines an axis vector.
variable: Integer that indicates the variable (in [1,n]) for which the estimates of high-dimensional data will be exact. Default: variable = 1.
solver: String indicating a package or method for solving the optimization problem. It can be "formula" (default), where the solution is obtained through a closed-form formula, or "CVXR".

Value

A list with the three following entries:

P: A numeric N x m matrix containing the mapped points. Each row is the low-dimensional representation of a data observation in X.
status: A vector of length N where the i-th element contains the status of the chosen solver when calculating the mapping of the i-th data observation. The type of the elements depends on the particular chosen solver.
objval: The numeric objective value associated with the solution to the optimization problem, considering matrix norms.

The output status vector returns the 2-norm condition number of V. If the chosen solver fails to map the data (i.e., fails to solve the related optimization problem), P will contain NA (not available) values. In that case, objval will also be NA.

Details

ara_exact_l2() computes low-dimensional point representations of high-dimensional numerical data (X) according to the data visualization method "Adaptable Radial Axes" (M. Rubio-Sánchez, A. Sanchez, and D. J. Lehmann (2017), doi: 10.1111/cgf.13196), which describes a collection of convex norm optimization problems aimed at minimizing estimates of original values in X through dot products of the mapped points with the axis vectors (rows of V). This particular function solves the constrained optimization problem in Eq. (13), for the squared-Euclidean norm. Its equality constraint forces estimates to be exact for one of the data variables. The problem admits closed-form solutions.

References

M. Rubio-Sánchez, A. Sanchez, D. J. Lehmann: Adaptable radial axes plots for improved multivariate data visualization. Computer Graphics Forum 36, 3 (2017), 389–399. doi:10.1111/cgf.13196

Examples

# Load data
data("auto_mpg", package = "ascentTraining")

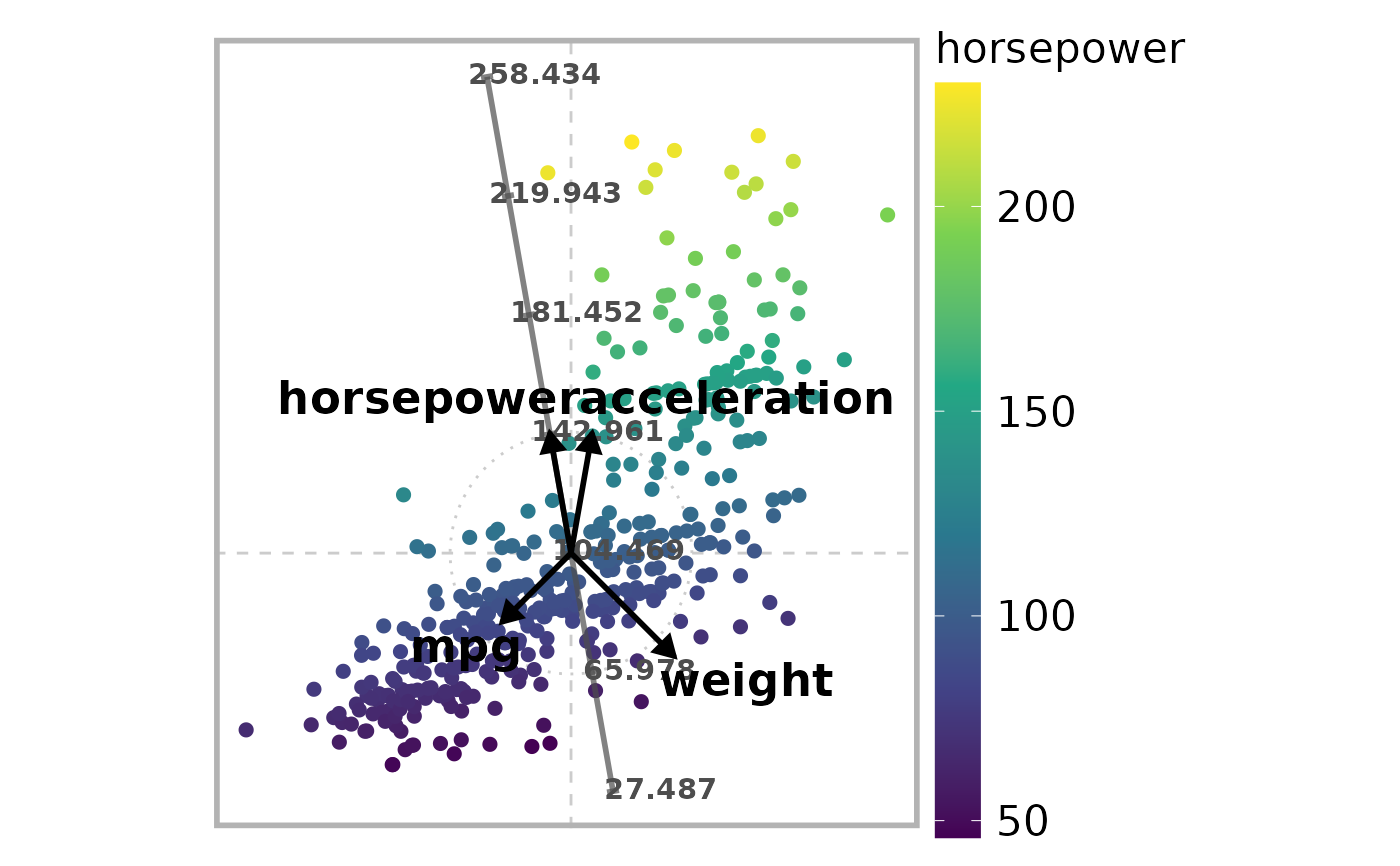
# Define subset of (numerical) variables
# 1:"mpg", 4:"horsepower", 5:"weight", 6:"acceleration"
selected_variables <- c(1, 4, 5, 6)

# Retain only selected variables and rename dataset as X
X <- auto_mpg[, selected_variables] # Select a subset of variables
rm(auto_mpg)
#> Warning: object 'auto_mpg' not found

# Remove rows with missing values from X
N <- nrow(X)
rows_to_delete <- NULL
for (i in 1:N) {
  if (sum(is.na(X[i, ])) > 0) {
    rows_to_delete <- c(rows_to_delete, -i)
  }
}
X <- X[rows_to_delete, ]

# Convert X to matrix
X <- apply(as.matrix.noquote(X), 2, as.numeric)

# Standardize data
Z <- scale(X)

# Define axis vectors (2-dimensional in this example)
r <- c(0.8, 1, 1.2, 1)
theta <- c(225, 100, 315, 80) * 2 * pi / 360
V <- geometry::pol2cart(theta, r)

# Select variable for exact estimates, and use it for coloring the embedded
# points
n <- nrow(V)
variable <- sample(1:n, 1)

# Compute the mapping
mapping <- ara_exact_l2(
  Z,
  V,
  variable = variable,
  solver = "formula"
)

# Select variables with labeled axis lines on ARA plot
axis_lines <- variable

# Draw the ARA plot
draw_ara_plot_2d_standardized(
  Z,
  X,
  V,
  mapping$P,
  axis_lines = axis_lines,
  color_variable = variable
)
#> [1] 0